- Aggregation of identical sequences (in order to save memory and cluster a bigger number of sequences).
- Computation of several clustering quality measure.
- Methods facilitating the choice of the number of groups and cluster algorithm based on cluster quality measures.
- Clustering of weighted data using a distance matrix.
- An optimized PAM algorithm.
- Graphical representation of hierarchical clustering of state sequence (you need to install GraphViz http://www.graphviz.org )
News
- 16.01.2014 New WeightedCluster version 1.2: Speed improvement, bootstrapping cluster quality measure and automatic cluster algorithm comparison using function wcCmpCluster.
WeightedCluster Manuals
The WeightedCluster detailled manual (also available in French) provides a step-by-step guide to creating typologies of sequences for the social sciences using the WeightedCluster library. It also discusses the building of typologies of sequences in the social sciences and the assumptions underlying this method.The full reference of the manual is:
Studer, Matthias (2013). WeightedCluster Library Manual: A practical guide to creating typologies of trajectories in the social sciences with R. LIVES Working Papers, 24. DOI: 10.12682/lives.2296-1658.2013.24.
A short preview in English is available below and here in PDF: WeightedCluster Preview
Citing WeightedCluster
Thank you for citing the WeightedCluster manual when presenting analyses realized with the help of WeightedCluster.Studer, Matthias (2013). WeightedCluster Library Manual: A practical guide to creating typologies of trajectories in the social sciences with R. LIVES Working Papers, 24. DOI: 10.12682/lives.2296-1658.2013.24.
Help and Contact
For any question, suggestion, feature request or bug report, please feel free to contact Matthias Studer matthias.studer@unige.chPreview
Installation
Some functions of WeightedCluster require the free GraphViz program. It needs to be installed before launching R for these functions to work properly.
The WeightedCluster library can be installed and loaded using the following commands:
install.packages("WeightedCluster") library(WeightedCluster)
An illustrative example
In this preview, we use the dataset from McVicar and Anyadike 2002 which is distributed with the TraMineR library. This dataset contains sequences of school-to-work transitions in Northern Ireland. The dataset is loaded using :
data(mvad)
wcAggregateCases allows us to identify and aggregate identical state sequences (which are in columns 17:86. We print out the basic information about the aggregation and create the uniqueMvad object which contains only unique sequences.
aggMvad <- wcAggregateCases(mvad[, 17:86]) print(aggMvad)
## Number of disaggregated cases: 712 ## Number of aggregated cases: 490 ## Average aggregated cases: 1.45 ## Average (weighted) aggregation: 1.45
uniqueMvad <- mvad[aggMvad$aggIndex, 17:86]
Using the unique sequence dataset, we build a sequence object and compute dissimilarities between sequences (on this topic, see the TraMineR vignette) . The vector aggMvad$aggWeights store the number of replication of each unique sequence. It is thus used as unique sequence weight.
mvad.seq <- seqdef(uniqueMvad, weights = aggMvad$aggWeights) diss <- seqdist(mvad.seq, method = "HAM")
Hierarchical clustering
We can regroup similar sequences using hierarchical clustering with "average" method using weights (aggMvad$aggWeights) (any method may be used).
averageClust <- hclust(as.dist(diss), method = "average", members = aggMvad$aggWeights)
The agglomeration schedule can be represented graphically as a tree using:
averageTree <- as.seqtree(averageClust, seqdata = mvad.seq, diss = diss, ncluster = 6) seqtreedisplay(averageTree, type = "d", border = NA, showdepth = TRUE)
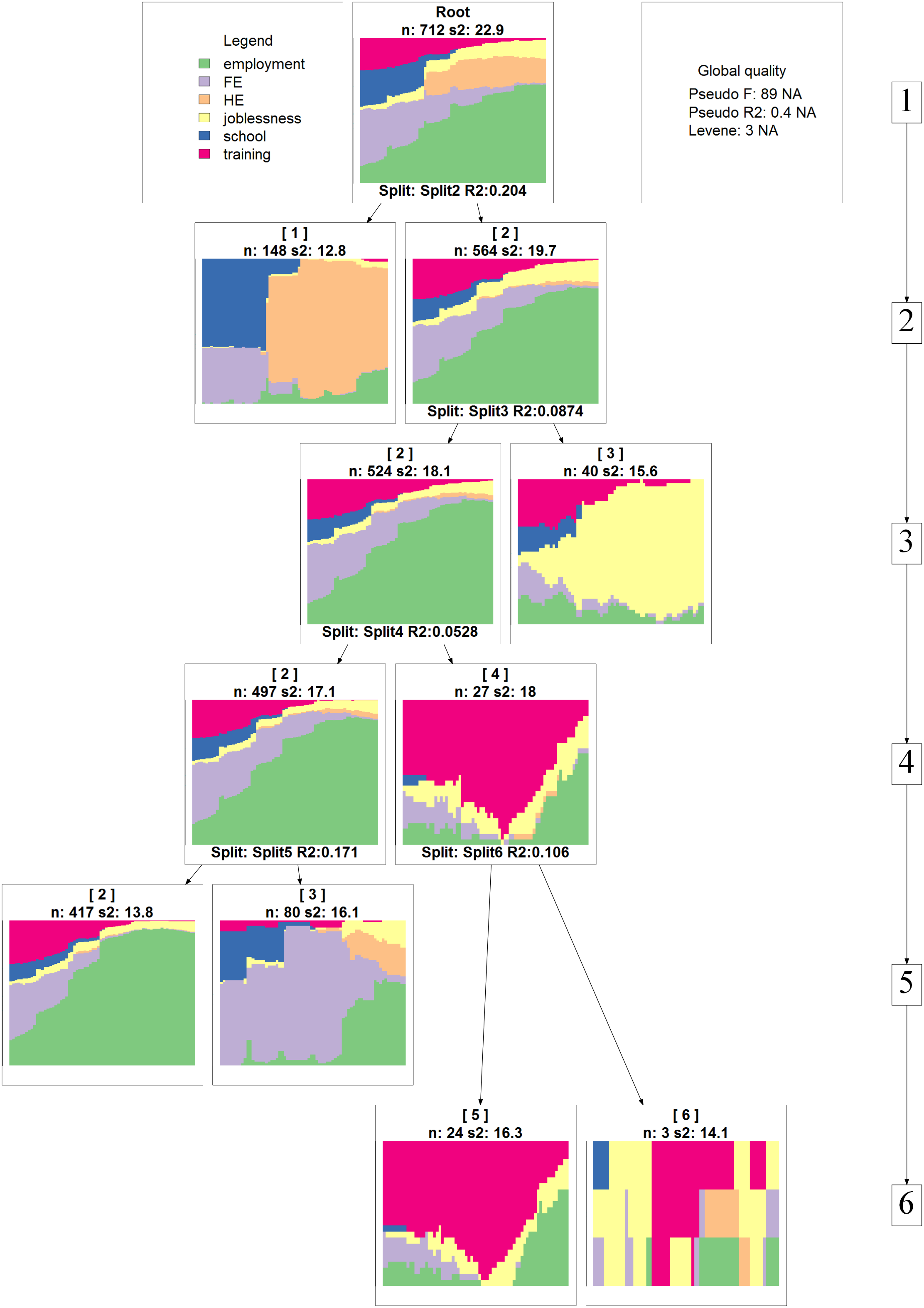
Cluster quality
We can automatically compute several clustering quality measures (presented in table below) for a range of numbers of groups: 2 until ncluster=10.
avgClustQual <- as.clustrange(averageClust, diss, weights = aggMvad$aggWeights, ncluster = 10)
Available quality measures
| Name | Abrv. | Range | Min/Max | Interpretation |
|---|---|---|---|---|
| Point Biserial Correlation | PBC | [-1;1] | Max | Capacity of the clustering to reproduce the original distance matrix. |
| Hubert's Gamma | HG | [-1;1] | Max | Capacity of the clustering to reproduce the original distance matrix (Order of magnitude). |
| Hubert's Somers D | HGSD | [-1;1] | Max | Same as above, taking into account ties in the distance matrix. |
| Hubert's C | HC | [0;1] | Min | Gap between the current quality of clustering and the best possible quality for this distance matrix and number of groups. |
| Average Silhouette Width | ASW | [-1;1] | Max | Coherence of the assignments. A high coherence indicates high between groups distances and high intra group homogeneity. |
| Calinski-Harabasz index | CH | [0;+∞[ | Max | Pseudo F computed from the distances. |
| Calinski-Harabasz index | CHsq | [0;+∞[ | Max | Idem, using the squared distances. |
| Pseudo R2 | R2 | [0;1] | Max | Share of the discrepancy explained by the clustering. |
| Pseudo R2 | R2sq | [0;1] | Max | Idem, using the squared distances. |
The results can be plotted and used to identify the best number of groups (you can also print them).
plot(avgClustQual)
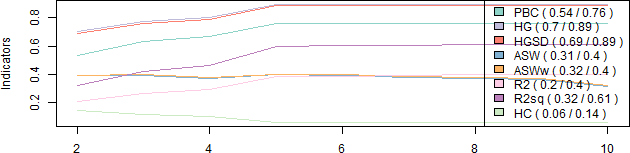
It is usually easier to choose the number of groups based on standardized scores. Here, five groups seems to be a good solution.
plot(avgClustQual, norm = "zscore")
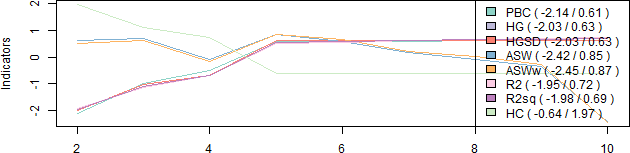
Alternatively, we can retrieve the two best solutions according to each quality measure:
summary(avgClustQual, max.rank = 2)
## 1. N groups 1. stat 2. N groups 2. stat ## PBC 10 0.7616 9 0.761 ## HG 10 0.8939 9 0.893 ## HGSD 10 0.8910 9 0.890 ## ASW 5 0.3966 3 0.393 ## ASWw 5 0.4010 6 0.396 ## CH 2 181.9886 3 126.780 ## R2 10 0.3980 9 0.396 ## CHsq 2 338.5174 5 262.451 ## R2sq 10 0.6145 9 0.613 ## HC 10 0.0598 9 0.060
PAM clustering
The WeightedCluster library also provides an optimized PAM algorithm. We can automatically compute PAM cluster for a range of numbers of groups using:
pamClustRange <- wcKMedRange(diss, kvals = 2:10, weights = aggMvad$aggWeights)
As before, we can plot the quality measures of each solution (not shown here) or retrieve the two best solutions according to each quality measure using:
summary(pamClustRange, max.rank = 2)
## 1. N groups 1. stat 2. N groups 2. stat ## PBC 2 0.619 4 0.618 ## HG 10 0.845 9 0.845 ## HGSD 10 0.842 9 0.842 ## ASW 2 0.411 9 0.370 ## ASWw 2 0.412 9 0.378 ## CH 2 200.286 3 151.245 ## R2 10 0.590 9 0.576 ## CHsq 2 394.893 4 310.881 ## R2sq 10 0.786 9 0.774 ## HC 9 0.100 10 0.104
Keeping a solution
The objets returned by as.clustrange or wcKMedRange contain a data.frame with cluster membership (named clustering). For instance, we can plot the sequences according to PAM clustering in 5 groups using:
seqdplot(mvad.seq, group = pamClustRange$clustering$cluster5, border = NA)
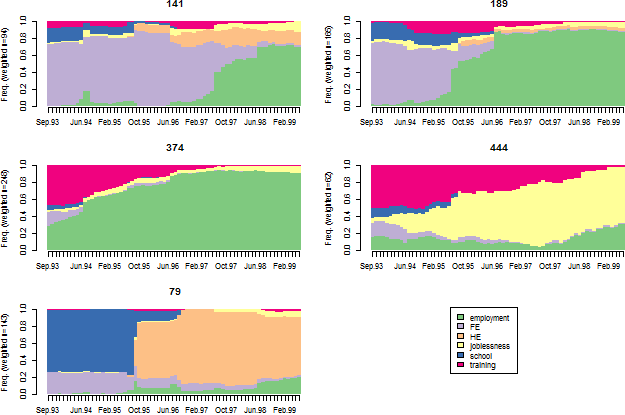
Disaggregating data
Once the sequences have been regrouped, it is often useful to “disaggregate” the data. For instance, we may want to add the cluster membership in the original data set (i.e. before unique sequences were identified). This allows us to cross-tabulate cluster membership and father unemployment (variable funemp). This operation is performed using aggMvad$disaggIndex which stores the index of each unique sequence in the original dataset.
uniqueCluster5 <- avgClustQual$clustering$cluster5 mvad$cluster5 <- uniqueCluster5[aggMvad$disaggIndex] table(mvad$funemp, mvad$cluster5)
## ## 1 2 3 4 5 ## no 134 348 70 24 19 ## yes 14 69 10 16 8
